Archivo del autor: AlexFrz

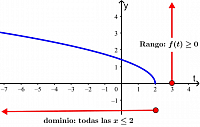
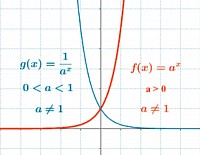
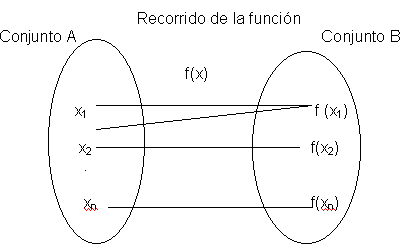
ᴇʟ ᴅᴏᴍɪɴɪᴏ ᴅᴇ ᴜɴᴀ «ғᴜɴᴄɪᴏɴ» ғ (x) ᴇs ᴇʟ ᴄᴏɴᴊᴜɴᴛᴏ ᴅᴇ ᴛᴏᴅᴏs ʟᴏs ᴠᴀʟᴏʀᴇs ᴘᴀʀᴀ ʟᴏs ᴄᴜᴀʟᴇs ʟᴀ ғᴜɴᴄɪᴏ́ɴ ᴇsᴛᴀ́ ᴅᴇғɪɴɪᴅᴀ ʏ ᴇʟ ʀᴀɴɢᴏ ᴅᴇ ʟᴀ ғᴜɴᴄɪᴏ́ɴ ᴇs ᴇʟ ᴄᴏɴᴊᴜɴᴛᴏ ᴅᴇ ᴛᴏᴅᴏs ʟᴏs ᴠᴀʟᴏʀᴇs ϙᴜᴇ ғᴏʀᴍᴀ ғ

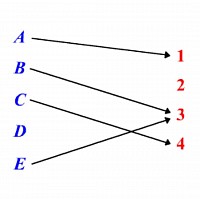
ᴇᴊᴇᴍᴘʟᴏ ᴀ–1. ʙ–3. ᴄ–4. ᴇ–3.

ᴀϙᴜɪ́ ᴇʟ ᴅᴏᴍɪɴɢᴏ ᴇs ᴇʟ ᴄᴏɴᴊᴜɴᴛᴏ {ᴀ,ʙ,ᴄ,ᴅ} ᴅ ɴᴏ ᴇsᴛᴀ́ ᴇɴ ᴇʟ ᴅᴏᴍɪɴɪᴏ ʏᴀ ϙᴜᴇ ʟᴀ ғᴜɴᴄɪᴏɴ ɴᴏ ᴇsᴛᴇ ᴅᴇɴᴛɪғɪᴄᴀᴅᴀ ᴘᴀʀᴀ ᴅ

ᴇʟ ᴇʟ ʀᴀɴɢᴏ ᴅᴇʟ ᴄᴏɴᴊᴜɴᴛᴏ {1,2,4} 2 ɴᴏ ᴇsᴛᴀ́ ᴇɴ ᴇʟ ʀᴀɴɢᴏ ,ʏᴀ ϙᴜᴇ ɴᴏ ʜᴀʏ ʟᴇᴛʀᴀ ᴇɴ ᴇʟ ᴅᴏᴍɪɴɪᴏ ϙᴜᴇ sᴇ ᴇɴʟᴀᴢᴀ ᴄᴏɴ ᴇʟ 2

ᴇʟ ᴅᴏᴍɪɴɪᴏ ᴅᴇ ʟᴀ ғᴜɴᴄɪᴏ́ɴ ғ x = 1/x ᴇs ᴛᴏᴅᴏs ʟᴏs ɴᴜ́ᴍᴇʀᴏs ʀᴇᴀʟᴇs, ᴇxᴄᴇᴘᴛᴏ ᴇʟ ᴄᴇʀᴏ ʏᴀ ϙᴜᴇ ᴇɴ x = 0 ʟᴀ ғᴜɴᴄɪᴏ́ɴ ɴᴏ ᴇsᴛᴀ́ ᴅᴇғɪɴɪᴅᴀ

ᴇʟ ʀᴀɴɢᴏ ᴛᴀᴍʙɪᴇ́ɴ ᴇs ᴇʟ ᴛᴏᴅᴏs ʟᴏs ɴᴜ́ᴍᴇʀᴏs ʀᴇᴀʟᴇs ᴇxᴄᴇᴘᴛᴏ ᴇʟ ᴄᴇʀᴏ

---

ᴇʟ ᴅᴏᴍɪɴɪᴏ ᴅᴇ ᴜɴᴀ ғᴜɴᴄɪᴏ́ɴ ғ ( x ) ᴇs ᴇʟ ᴄᴏɴᴊᴜɴᴛᴏ ᴅᴇ ᴛᴏᴅᴏs ʟᴏs ᴠᴀʟᴏʀᴇs ᴘᴀʀᴀ ʟᴏs ᴄᴜᴀʟᴇs ʟᴀ ғᴜɴᴄɪᴏ́ɴ ᴇsᴛᴀ́ ᴅᴇғɪɴɪᴅᴀ, ʏ ᴇʟ ʀᴀɴɢᴏ ᴅᴇ ʟᴀ ғᴜɴᴄɪᴏ́ɴ ᴇs ᴇʟ ᴄᴏɴᴊᴜɴᴛᴏ ᴅᴇ ᴛᴏᴅᴏs ʟᴏs ᴠᴀʟᴏʀᴇs ϙᴜᴇ ғ ᴛᴏᴍᴀ.

(ᴇɴ ɢʀᴀᴍᴀ́ᴛɪᴄᴀ, ᴘʀᴏʙᴀʙʟᴇᴍᴇɴᴛᴇ ʟᴇ ʟʟᴀᴍᴇ ᴀʟ ᴅᴏᴍɪɴɪᴏ ᴇʟ ᴄᴏɴᴊᴜɴᴛᴏ ʀᴇᴇᴍᴘʟᴀᴢᴏ ʏ ᴀʟ ʀᴀɴɢᴏ ᴇʟ ᴄᴏɴᴊᴜɴᴛᴏ sᴏʟᴜᴄɪᴏ́ɴ. ϙᴜɪᴢᴀ́ ᴛᴀᴍʙɪᴇ́ɴ ᴇsᴛᴏs ʜᴀɴ sɪᴅᴏ ʟʟᴀᴍᴀᴅᴏs ʟᴀ ᴇɴᴛʀᴀᴅᴀ ʏ sᴀʟɪᴅᴀ ᴅᴇ ʟᴀ ғᴜɴᴄɪᴏ́ɴ.)

ʟᴏs ᴅᴏᴍɪɴɪᴏs ᴘᴜᴇᴅᴇɴ ᴛᴀᴍʙɪᴇ́ɴ ᴇsᴛᴀʀ ᴇxᴘʟɪ́ᴄɪᴛᴀᴍᴇɴᴛᴇ ᴇsᴘᴇᴄɪғɪᴄᴀᴅᴏs, sɪ ʜᴀʏ ᴠᴀʟᴏʀᴇs ᴘᴀʀᴀ ʟᴏs ᴄᴜᴀʟᴇs ʟᴀ ғᴜɴᴄɪᴏ́ɴ ᴘᴜᴅɪᴇʀᴀ ᴇsᴛᴀʀ ᴅᴇғɪɴɪᴅᴀ, ᴘᴇʀᴏ ϙᴜᴇ ɴᴏ ᴅᴇsᴇᴀᴍᴏs ᴄᴏɴsɪᴅᴇʀᴀʀʟᴏs ᴘᴏʀ ᴀʟɢᴜɴᴀ ʀᴀᴢᴏ́ɴ..)

El dominio de una función es el conjunto de objetos a los que la función asigna valores. El rango es el conjunto de valores obtenidos

1.-ᴀʀᴍᴀ ᴜɴᴀ ᴛᴀʙʟᴀ ᴅᴇ ᴠᴀʟᴏʀᴇs, ᴛᴀʙᴜʟᴀɴᴅᴏ ᴅɪғᴇʀᴇɴᴛᴇs ᴠᴀʟᴏʀᴇs ᴅᴇ “x”, “ʏ”, ʏ ᴄᴏʟᴏᴄᴀɴᴅᴏ ʟᴏs ᴘᴀʀᴇs ᴏʀᴅᴇɴᴀᴅᴏs.

2.-ʜᴀɢᴀᴍᴏs ᴇʟ ᴇᴊᴇᴍᴘʟᴏ ᴅᴇ ʟᴀ ғᴜɴᴄɪᴏ́ɴ: ʏ = 2x + 1. x. -2. -1. +1. +2. ʏ. -3. -1. +1. +3. +5. (x;ʏ) (-2 ; -3) …

3.-ᴄᴏʟᴏᴄᴀ ʟᴏs ᴘᴀʀᴇs ᴏʀᴅᴇɴᴀᴅᴏs ᴇɴ ᴇʟ ᴘʟᴀɴᴏ ᴄᴀʀᴛᴇsɪᴀɴᴏ.

4.- ᴜɴᴇ ʟᴏs ᴘᴜɴᴛᴏs ғᴏʀᴍᴀɴᴅᴏ ʟᴀ ᴄᴜʀᴠᴀ.

ᴄᴏɴ ᴇsᴛᴏs ᴘᴀsᴏs, ᴘᴜᴇᴅᴇs ɢʀᴀғɪᴄᴀʀ ᴄᴜᴀʟϙᴜɪᴇʀ ғᴜɴᴄɪᴏ́ɴ, ʏᴀ sᴇᴀ ʟɪɴᴇᴀʟ, ᴄᴜᴀᴅʀᴀ́ᴛɪᴄᴀ, ᴇxᴘᴏɴᴇɴᴄɪᴀʟ, ᴠᴀʟᴏʀ ᴀʙsᴏʟᴜᴛᴏ, ᴇɴᴛʀᴇ ᴏᴛʀᴀs. ᴍᴀ́s ᴀᴅᴇʟᴀɴᴛᴇ, ᴠᴇʀᴇᴍᴏs ᴏᴛʀᴀs ғᴜɴᴄɪᴏɴᴇs ᴅᴇ ᴍᴀʏᴏʀ ᴅɪғɪᴄᴜʟᴛᴀᴅ, ᴀɴᴀʟɪᴢᴀɴᴅᴏ ᴅᴏᴍɪɴɪᴏ, ʀᴀɴɢᴏ, ɪɴᴛᴇʀsᴇᴄᴄɪᴏɴᴇs, ᴘᴀʀɪᴅᴀᴅ, ᴀsɪ́ɴᴛᴏᴛᴀs ʏ ᴍᴀ́s.

El gráfico de una función es una representación visual del comportamiento de una función en un plano x-y. Los gráficos nos ayudan a comprender los diferentes aspectos de una función, lo cual sería difícil con solo mirar a la ecuación. Puedes graficar miles de ecuaciones y cada una tiene una fórmula diferente. Sin embargo, siempre hay formas de graficar una función si olvidas los pasos exactos para ese tipo específico de función.

ʟᴀs ᴇᴠᴀʟᴜᴀᴄɪᴏɴᴇs ᴇsᴄʀɪᴛᴀs ᴇɴ ɴᴏᴛᴀᴄɪᴏ́ɴ ᴅᴇ ғᴜɴᴄɪᴏ́ɴ ᴛᴀᴍʙɪᴇ́ɴ ᴘᴜᴇᴅᴇɴ sᴇʀ ᴇᴠᴀʟᴜᴀᴅᴀs ᴄᴏɴ ʟᴀ ɴᴏᴛᴀᴄɪᴏ́ɴ ᴅᴇ ғᴜɴᴄɪᴏ́ɴ ᴘᴏᴅʀɪ́ᴀs ᴠᴇʀ ᴘʀᴏʙʟᴇᴍᴀs ᴄᴏᴍᴏ ᴇsᴛᴏs

ᴅᴀᴅᴀ ғ(x)=4x+1, ᴇɴᴄᴏɴᴛʀᴀʀ ғ(2)

ᴇʟ ᴘʀᴏʙʟᴇᴍᴀ sᴇ ʟᴇᴇ ᴄᴏᴍᴏ ᴅᴀᴅᴀ ғ ᴅᴇ x = 4x + 1 ᴇɴᴄᴏɴᴛʀᴀʀ ғ ᴅᴇ 2, sɪ́ ᴇsᴛᴀ́ ʙɪᴇɴ ʟᴀ ɴᴏᴛᴀᴄɪᴏ́ɴ ʏ ʟᴀs ᴘᴀʟᴀʙʀᴀs sᴏɴ ᴅɪғᴇʀᴇɴᴛᴇs, ᴇʟ ᴘʀᴏᴄᴇsᴏ ᴅᴇ ᴇᴠᴀʟᴜᴀʀ ᴜɴᴀ ғᴜɴᴄɪᴏ́ɴ ᴇs ᴇʟ ᴍɪsᴍᴏ ᴅᴇ ᴇᴠᴀʟᴜᴀʀ ᴜɴᴀ ᴇᴄᴜᴀᴄɪᴏ́ɴ ᴇɴ ᴀᴍʙᴏs ᴄᴀsᴏs sᴜsᴛɪᴛᴜʏᴇɴᴛᴇs 2 ᴘᴏʀ x ,ᴍᴀ́s ʙɪᴇɴ, ʟᴀ ɴᴏᴛᴀᴄɪᴏ́ɴ sɪɢɴɪғɪᴄᴀ ғ ᴅᴇ x ᴏ ʟᴀ ғᴜɴᴄɪᴏ́ɴ ᴅᴇ x ᴘᴀʀᴀ ᴇᴠᴀʟᴜᴀʀ ʟᴀ ғᴜɴᴄɪᴏ́ɴ ᴛᴏᴍᴀ ᴇʟ ᴠᴀʟᴏʀ ᴅᴀᴅᴏ ᴅᴇ x ʏ sɪ sᴜsᴛɪᴛᴜʏᴇs ᴇsᴇ ᴠᴀʟᴏʀ ᴘᴏʀ x ᴇɴ ʟᴀ ᴇxᴘʀᴇsɪᴏ́ɴ

Ejemplos

f(x) = 4x + 1
f(2) = 4(2) + 1 = 8 + 1 = 9

ғᴜɴᴄɪᴏɴᴇs ᴀʟɢᴇʙʀᴀɪᴄᴀs: ᴇɴ ʟᴀs ғᴜɴᴄɪᴏɴᴇs ᴀʟɢᴇʙʀᴀɪᴄᴀs ʟᴀs ᴏᴘᴇʀᴀᴄɪᴏɴᴇs ϙᴜᴇ ʜᴀʏ ϙᴜᴇ ᴇᴊᴇᴄᴜᴛᴀʀ ᴄᴏɴ ʟᴀ ᴠᴀʀɪᴀʙʟᴇ ɪɴᴅᴇᴘᴇɴᴅɪᴇɴᴛᴇ sᴏɴ: ʟᴀ ᴀᴅɪᴄɪᴏ́ɴ , sᴜsᴛʀᴀᴄᴄɪᴏ́ɴ, ᴍᴜʟᴛɪᴘʟᴀᴄɪᴏɴ , ᴅɪᴠɪsɪᴏ́ɴ , ᴘᴏᴛᴇɴᴄɪᴀᴄɪᴏ́ɴ ʏ ʀᴀᴅɪᴀᴄɪᴏɴ

ғᴜɴᴄɪᴏɴᴇs ᴇxᴘʟɪ́ᴄɪᴛᴀs: sᴇ ᴘᴜᴇᴅᴇɴ ᴏʙᴛᴇɴᴇʀ ʟᴀs ɪᴍᴀ́ɢᴇɴᴇs ᴅᴇ x ᴘᴏʀ sɪᴍᴘʟᴇ sɪᴛᴜᴀᴄɪᴏ́ɴ 

ғᴜɴᴄɪᴏɴᴇs ɪᴍᴘʟɪ́ᴄɪᴛᴀs: ɴᴏ sᴇ ᴘᴜᴇᴅᴇɴ ᴏʙᴛᴇɴᴇʀ ʟᴀs ɪᴍᴀ́ɢᴇɴᴇs ᴅᴇ x ᴘᴏʀ sɪᴍᴘʟᴇ sɪᴛᴜᴀᴄɪᴏ́ɴ, sɪɴᴏ ϙᴜᴇ ᴇs ᴘʀᴇᴄɪsᴏ ᴇғᴇᴄᴛᴜᴀʀ ᴏᴘᴇʀᴀᴄɪᴏɴᴇs 

ғᴜɴᴄɪᴏɴᴇs ᴘᴏʟɪɴᴏ́ᴍɪᴄᴀs: sᴜ ᴅᴏᴍɪɴɪᴏ ᴇs ʀ ,ᴇs ᴅᴇᴄɪʀ,ᴄᴜᴀʟϙᴜɪᴇʀ ɴᴜ́ᴍᴇʀᴏ ʀᴇᴀʟ ᴛɪᴇɴᴇ ɪᴍᴀɢᴇɴ ᴄᴜᴀ́ɴᴅᴏ sᴇ ᴛʀᴀʙᴀᴊᴀ ᴄᴏɴ ᴀ́ʟɢᴇʙʀᴀ, ʟᴀs ғᴏʀᴍᴀs sᴏɴ ᴀʟɢᴏ ɪɴᴄʟᴜʏᴇɴᴛᴇs, ᴇᴊᴇᴍᴘʟᴏ, ɪᴏɴᴀʟᴇs ᴄᴏᴄɪᴇɴᴛᴇ ᴅᴇ ᴅᴏs ᴘᴏʟɪɴᴏᴍɪᴏs, ᴇsᴛᴇ ᴘᴜᴇᴅᴇ ᴇsᴄʀɪʙɪʀsᴇ ᴄᴏᴍᴏ ᴇʟ ᴄᴏᴄɪᴇɴᴛᴇ ᴅᴇ ʏ ᴇɴᴛʀᴇ ʟᴀ ᴜɴɪᴅᴀᴅ ,ᴘᴏʀ ʟᴀ ᴏᴛʀᴀ ᴘᴀʀᴛᴇ ʟᴏs ᴘᴏʟɪɴᴏᴍɪᴏs sᴏɴ ᴛᴀᴍʙɪᴇ́ɴ ᴘᴏʟɪɴᴏᴍɪᴏs ᴇɴ ᴜɴ sᴇɴᴛɪᴅᴏ ɢᴇɴᴇ́ʀɪᴄᴏ,ᴄᴏɴ ʟᴀ ᴄᴀʀᴀᴄᴛᴇʀɪᴢᴀᴄɪᴏ́ɴ ᴅᴇ ᴘᴏsᴇᴇʀ ᴜɴ sᴏʟᴏ ᴛᴇʀᴍɪɴᴏ 

---

La definición de función se dá enseguida. Función: Una función es una regla de correspondencia entre dos conjuntos de tal manera que a cada elemento del primer conjunto le corresponde uno y sólo un elemento del segundo conjunto. Al primer conjunto (el conjunto D) se le da el nombre de dominio.

ᴇs ᴜɴᴀ ʀᴇɢʟᴀ ᴅᴇ ᴄᴏʀʀᴇsᴘᴏɴᴅᴇɴᴄɪᴀ ᴇɴᴛʀᴇ ᴅᴏs ᴄᴏɴᴊᴜɴᴛᴏs ᴅᴇ ᴛᴀʟ ᴍᴀɴᴇʀᴀ ϙᴜᴇ ᴀ ᴄᴀᴅᴀ ᴇʟᴇᴍᴇɴᴛᴏ ᴅᴇʟ ᴘʀɪᴍᴇʀ ᴄᴏɴᴊᴜɴᴛᴏ ʟᴇ ᴄᴏʀʀᴇsᴘᴏɴᴅᴇ 1 ʏ ᴜɴ sᴏʟᴏ ᴇʟᴇᴍᴇɴᴛᴏ ᴅᴇʟ ᴄᴏɴᴊᴜɴᴛᴏ, ᴀʟ ᴘʀɪᴍᴇʀᴏ , sᴇ ʟᴇ ᴅᴀ ᴇʟ ɴᴏᴍʙʀᴇ ᴅᴇ ᴅᴏᴍɪɴɪo