𝙲𝚄𝙰𝙻 𝙴𝚂 𝙴𝙻 𝙼𝙴𝚃𝙾𝙳𝙾 𝙿𝙰𝚁𝙰 𝙶𝚁𝙰𝙵𝙸𝙲𝙰𝚁 𝙻𝙰𝚂 𝙵𝚄𝙽𝙲𝙸𝙾𝙽𝙴𝚂

1.-ᴀʀᴍᴀ ᴜɴᴀ ᴛᴀʙʟᴀ ᴅᴇ ᴠᴀʟᴏʀᴇs, ᴛᴀʙᴜʟᴀɴᴅᴏ ᴅɪғᴇʀᴇɴᴛᴇs ᴠᴀʟᴏʀᴇs ᴅᴇ “x”, “ʏ”, ʏ ᴄᴏʟᴏᴄᴀɴᴅᴏ ʟᴏs ᴘᴀʀᴇs ᴏʀᴅᴇɴᴀᴅᴏs.

2.-ʜᴀɢᴀᴍᴏs ᴇʟ ᴇᴊᴇᴍᴘʟᴏ ᴅᴇ ʟᴀ ғᴜɴᴄɪᴏ́ɴ: ʏ = 2x + 1. x. -2. -1. +1. +2. ʏ. -3. -1. +1. +3. +5. (x;ʏ) (-2 ; -3) …

3.-ᴄᴏʟᴏᴄᴀ ʟᴏs ᴘᴀʀᴇs ᴏʀᴅᴇɴᴀᴅᴏs ᴇɴ ᴇʟ ᴘʟᴀɴᴏ ᴄᴀʀᴛᴇsɪᴀɴᴏ.

4.- ᴜɴᴇ ʟᴏs ᴘᴜɴᴛᴏs ғᴏʀᴍᴀɴᴅᴏ ʟᴀ ᴄᴜʀᴠᴀ.

ᴄᴏɴ ᴇsᴛᴏs ᴘᴀsᴏs, ᴘᴜᴇᴅᴇs ɢʀᴀғɪᴄᴀʀ ᴄᴜᴀʟϙᴜɪᴇʀ ғᴜɴᴄɪᴏ́ɴ, ʏᴀ sᴇᴀ ʟɪɴᴇᴀʟ, ᴄᴜᴀᴅʀᴀ́ᴛɪᴄᴀ, ᴇxᴘᴏɴᴇɴᴄɪᴀʟ, ᴠᴀʟᴏʀ ᴀʙsᴏʟᴜᴛᴏ, ᴇɴᴛʀᴇ ᴏᴛʀᴀs. ᴍᴀ́s ᴀᴅᴇʟᴀɴᴛᴇ, ᴠᴇʀᴇᴍᴏs ᴏᴛʀᴀs ғᴜɴᴄɪᴏɴᴇs ᴅᴇ ᴍᴀʏᴏʀ ᴅɪғɪᴄᴜʟᴛᴀᴅ, ᴀɴᴀʟɪᴢᴀɴᴅᴏ ᴅᴏᴍɪɴɪᴏ, ʀᴀɴɢᴏ, ɪɴᴛᴇʀsᴇᴄᴄɪᴏɴᴇs, ᴘᴀʀɪᴅᴀᴅ, ᴀsɪ́ɴᴛᴏᴛᴀs ʏ ᴍᴀ́s.

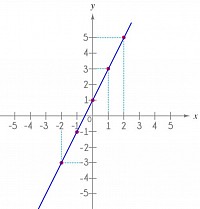
El gráfico de una función es una representación visual del comportamiento de una función en un plano x-y. Los gráficos nos ayudan a comprender los diferentes aspectos de una función, lo cual sería difícil con solo mirar a la ecuación. Puedes graficar miles de ecuaciones y cada una tiene una fórmula diferente. Sin embargo, siempre hay formas de graficar una función si olvidas los pasos exactos para ese tipo específico de función.